|
Xem bản PDF
Nhiều nhà toán học yêu âm nhạc và thích nghiên cứu vận dụng toán học vào các quy
luật của âm nhạc. Từ giữa thế kỷ trước, tháng 5-1942, gs Nguyễn Thúc Hào đã có
bài viết nghiên cứu về CÂY ĐÀN BẦU đăng trong tạp chí BÁO KHOA HỌC số 5-1942.Báo
do gs Nguyễn Xiển cùng các nhà khoa học yêu nước như gs Hoàng Xuân Hãn, gs Tạ
Quang Bửu, Ngụy Như Kon Tum..sáng lập. Chúng tôi đã có dịp giới thiệu với bạn
đọc trong tạp chí Toán Học Tuổi Trẻ số tháng 3-2006 .
Thế hệ tiếp theo, nhà giáo ưu tú Hoàng Trọng Thái (1940 – 2008), người nhiều
năm giảng dạy Hình học ở khoa toán trường ĐHSP Vinh cũng rất yêu âm nhạc, thích
tìm tòi , nghiên cứu vận dụng toán học vào âm nhạc. Nhớ lại những kỷ niệm sống
cùng anh trong những năm tháng đầy khó khăn ở các địa phương, nơi trường ĐHSP
Vinh sơ tán thời chống Mỹ cứu nước : Nghi Lộc, Thanh Chương, Thanh hóa. Nhân kỷ
niệm năm năm ngày “ ra đi ” của anh, tôi viết bài này có sử dụng một phần tư
liệu từ bài báo có nhan đề “ GAM ĐƠN GIẢN” của nhà toán học G.E. Shilov ( hình
như đăng trong tạp chí Kvant) do anh Tái dịch từ tiếng Nga sang tiếng Việt làm
tài liệu tham khảo. Bút tích của anh trên mấy trang giấy thủ công mầu nâu đã úa
thời chống Mỹ, đã gợi lại bản tính hiền dịu, nhẹ nhàng của anh, càng thương
tiếc anh. Bồi hồi xúc động trước sự “ra đi” quá đột ngột khi đang đang ấp ủ
nhiều kỳ vọng đóng góp cho sự nghiệp giáo dục nước nhà. Anh ra đi đã để lại một
khoảng trống lớn trong bạn bè, trong các đồng nghiệp của anh đã nhiều năm cùng
chung lưng đấu cật, cùng chia bùi sẻ ngọt với nhau ở trường ĐHSP Vinh. Những ai,
một thời đã từng là giáo viên hoặc sinh viên trường Vinh, nay ở Hà nội đều bị
hụt hẩng về sự thiếu vắng của một hạt nhân đoàn kết gắn bó với nhau- hạt nhân
HOÀNG TRỌNG THÁI.
1.
Xây dựng thang nhạc
a, Vài nét về âm thanh
Trước khi nói tới việc xây dựng thang âm
nhạc,chúng ta nói đôi nét về âm thanh, theo cách hiếu của vật lý:
Cơ sở toàn bộ âm nhạc là các âm, được xác định
bởi độ cao. Về phương diện vật lý, âm thanh là sóng đàn hồi lan truyền trong
không khí,( hoặc là quá trình rung trong không khí) với một tần số nào đó.
Đơn vị đo tần số là Héc(Hz) là số chu kỳ giao động trong một giây. Tần số càng
lớn thì âm càng cao. Tần số bé , âm thấp.
Âm thanh trầm nhất mà tai người có thể nghe
được có tần số 16Hz do đại phong cầm phát ra
nhưng rất ít khi dùng vì quá trầm , tai người
hầu như không nghe thấy .
Âm có tần số 27Hz ( lên octa 3 lần
sẽ được nốt Do1 ) rất rõ nhưng cũng ít khi dùng. Đó là nốt nhạc đầu
tiên phía trái đàn piano.
Âm 44 Hz(lên octa 3 lần sẽ được nốt Fa1)
là kỷ lục âm trầm nhất của ca sĩ giọng nam Caxpa Fexe hát ở thế kỷ 18
Âm 80Hz là âm trầm mà một ca sĩ bình thường
hát được.
Âm thanh mẫu phổ biến do âm thoa bình thường
phát ra nằm trong âm vực này, đó là nốt La1 (435Hz).
Các âm cao: 1000Hz, 1200Hz vẫn thuộc phạm
vi các nốt nhạc quen thuộc. Những nhạc cụ khác vượt quá phạm vi này gồm violon,
sáo,đại phong cầm, piano
Nữ ca sĩ Lucrexia Aghiari hát nổi nốt
Do4 (2018hec), . Nữ ca sĩ Pháp Mado- Robanh có thể hát thoải mái nốt
Re4( 2300Hz)
Các âm thanh từ 16000 Hz tới 20000Hz là siêu
âm , tai người không nghe thấy, người ta dùng vào các việc khác như khoan đá,
thăm dò đáy biển hoăc chụp ảnh các bộ phận trong y học….
b.
Xây dựng thang nhạc
Xây dựng thang nhạc không đơn giản như xây dựng thang nhiệt độ, đối với một
nhiệt kế thủy ngân . Lấy vạch ứng với độ đóng băng làm 00 và vạch
ứng với nhiệt độ khi nước sôi làm 1000 . Chia khoảng cách giữa hai
vạch đó ra 100 phần bằng nhau, đánh dấu từ 0 đến 100 ta được thang nhiệt độ bách
phân . Hoăc như cách chia 1m thành 100 phần bằng nhau, mõi phần có chiều dai
1cm. Thang nhạc khác, nếu ta chia một quảng tám từ một âm có tần số f0
đến âm có tần số 2f0
thành các quảng nhỏ bằng nhau như kiểu một nhiệt kế thì các âm thanh tạo nên sẽ
rất chói tai , người nghe không thể chịu nổi và phải làm cách khác.
Trước hết, thang nhạc phải thỏa mãn hai tiêu chuẩn:
*Số âm trong thang không lớn lắm . Trừ một số ít nhạc cụ như
violon, violonxel, người chơi có thể bấm vào bất kỳ chỗ nào trên cần để tạo ra
những âm thanh tùy ý, không có khoảng nhảy. Với những nhạc cụ khác, các phím đàn
ứng với một số không lớn âm cố định . Nếu nhiều quá, sẽ gây khó
khăn cho người sử dụng.
*.Hòa âm, các âm phát ra đồng thời trong thang phải hòa quyện
với nhau.nghe êm dịu , không có cảm giác chói tai.
Qua thực nghiệm, trước hết ta nhận thấy rằng âm có tần số f0
( nói gọn âm f0
) và âm 2f0
hòa với nhau tốt nhất. Vì thế, thang nhạc có âm f0
thì phải có âm 2f0, khoảng cách giữa chúng gọi là một Ôcta( một quảng tám) . Đặc trưng của
quảng giữa 2 âm là tỷ số tần số của chúng. Quảng tám có tý số là 2.
Ví dụ âm Do1 có tần số là 262, Do2(do1 lên một
octa) có tấn số là 523 , 523:262 = 2.
Âm có tần số bội 3 (3f) , bội 4, bội 5 cũng tham gia vào hòa âm, măc dầu rất yếu.
ta vẫn đưa vào thang.
Như
vậy, ngoài chủ âm ( âm đầu tiên của thang nhạc) f0
, các âm sau đây cũng nằm trong thang :
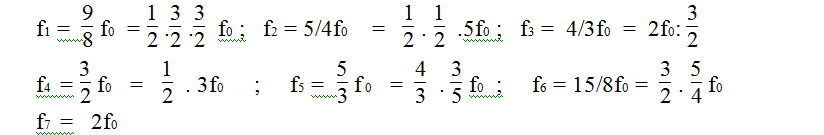
Các âm f0
,f1 ,
f 2,………,
f7
gọi là âm cơ bản.trong thang nhạc 7 bậc
( f0
, f1,
f2,
f3,
f4
, f5,
f6,
f7 =
2f0
) (1)
Các âm thanh khác sử dụng trong âm nhạc đều do các âm cơ bản trong thang
nhạc nâng cao lên hoặc hạ xuống một quảng 8 ( tần số giao đông của âm sai khác
một bội số của 2 hoặc 1/2) .
* Nhận xét: thang nhạc 7 bậc không đều, nếu cứ để nguyên không bổ
sung thêm một số âm nữa thì việc sử dụng sẽ gặp khó khăn, bởi vì khi chuyển
giai điệu lên cao hoặc xuống thầp một quảng tùy ý thì giai điệu bị méo, ví dụ
giai điệu bài “ ngày đầu tiên đi học “ của Nguyễn Ngọc Thiện
sol sol do sol mi , fa la fa la re…Nếu ta nâng giai điệu lên một
ton(giọng): la la re la fa , sol si sol si mi… ,sẽ bị
méo ở nốt fa . Hoặc bài Em yêu trường em của Hoàng
Vân : sol sol mị sol , la sol rẹ mị , rẹ mi rẹ mi sol do
…… Nếu ta nâng giai đíệu lên
một giọng : la la fa la , si la mi fa ,si la rẹ fa , mị fa mị fa la re
cũng bị méo. Để khắc phục điều đó, khi nâng cao lên hoặc hạ thấp thì giai điệu
không bị méo như các ví dụ trên. Ta phải xây dựng thang nhạc đều ( nghĩa là tỷ
số các âm liên tiếp liền nhau phải không đổi).
c. Nói qua vài nét về quá
trình dẫn đến một thang nhạc đều 12 bậc :
Người Hy lạp cổ xưa đã có công chia
âm giai thành các quãng tám( quãng tám là khoảng cách giữa các nốt có liên quan
gần gũi nhất) và chia mỗi quãng tám thành 12 bậc
Nhà toán học Pytago cũng phát
hiện thêm một quãng năm và nhận thấy rằng điểm cuối của quảng 5
thứ 12 gần trùng với quảng tám thứ bẩy.Điều này cho phép ông và những
người kế tục ông tạo nên một thang nhạc dựa trên quảng 8 và quảng 5, gọi là
thang nhạc Pytago
Thang nhạc Pytago tồn tại khá lâu,
nhưng không đáp ứng được giới âm nhạc. Nhược điểm chính của nó là các quảng 8
và quảng 5 không cùng một đơn vị đo, 12 lần quảng 5 dài hơn 7 lần quảng 8
:[(3/2)12 – (2)7 ] gần bằng 1,6 gần bằng 1/9
quảng giữa Re và Do, nên gây khó khăn cho việc lên giây đàn. Các nhạc sĩ và
các nhà bác học như Keple( nhà thiên văn học), Ơle( toán học) đã có nhiều cố
gắng nghiên cứu cải tiến nhưng không có két quả. Phải đến năm 1700, nhà toán học
kiêm nhạc sỹ người Đức Ăngdrê - Vecmâyơ đã đưa ra một cải tiến đơn
giản . Ông không dùng quãng 5 đúng mà lấy gần đúng tới mức có thể
chấp nhận được. Quảng ½ cung xuất hiện ( bằng khoảng giữa nốt Mi - Fa ( 349 –
330 =19)“ một cm âm nhạc “, nhưng , trong khi cm là một đơn vị đo tùy ý
thì quãng ½ cung lại rất thích hợp với các yêu cầu của âm học và thính giác của
con người. Quãng ½ cung tương đương với 1/12 quãng tám . Thang nhạc 12 bậc đều
này gọi là sự điều hòa ngang bằng hoặc gọi là âm giai ôn hòa , ngày nay là cơ
sở cho toàn bộ nền âm nhạc châu Âu. Mặc dầu vậy nó chỉ được công nhận sau đề
nghị của Băc và Ramô.
Xây dưng thang nhạc đều 12 bậc
Giả sử trong phạm vi một quảng 8 ,
những âm của thang là :
f0
<f1
< f2
<…..< f m-1
< fm
= 2f 0
Dãy những âm đó cũng làm thành một
giai điệu đơn giản . Bây giờ ta nâng giai điệu đó lên một bậc : f
1
, f2
, f3,…
.. fm,
fm+1
= 2f1.
Để giai điệu này không bị méo so với giai điệu xuất phát , cần có điều kiện:
f1 : f0
= f2 : f1 = f3 : f2 = ...... = fm
: fm-1 = fm+1 : fm
Dãy { f0
, f1
, …….fm-1,
fm }
là một cấp số nhân, công bội q; qm = 2
Để thuận tiện, ta chuyển dãy { f0
, f1,…..fm
} (1) thành
{log2f0,……,
log2fm
} (2)
Dãy này là một cấp số cộng có công sai d = 1/m.
Sau khi đặt log2f0
= A . Dãy trên sẽ là:
A, A+1/m,
A+2/m, ……., A+1 (3)
Vấn đề đặt ra bây giờ là chọn số
m như thế nao? Bằng các thí nghiệm trên giây đàn, người ta thấy rằng: ngoài tần
số f0
( âm có tần số giao động f0)
ra , các giao động có tần số 2f0,
3f0
, 4f0
đều tham gia, 5f0
thì nghe rất yếu.
Xét điều kiện Cùng với âm f0
trong thang nhạc phải có âm 3f0
.
Cũng có nghĩa là cần có âm 3/2f0,
trong khoảng (f0;2f0).
Ngoài số m ra, ta phải tìm được số k (k<m) sao cho
fk
= 3/2.f0
.
Đặt A = log2f0
và Lấy log2 cả
hai vế :
log2fk
= log2(3/2) + A.
Suy ra phải tìm các số nguyên m
và k
sao cho
log2(3/2)
= k/m
(4)
Điều kiện ( 4) tương đương 2k/m
= 3/2 hoặc 2k+m = 3m
Điều kiện này không thể thỏa mãn vì
vế trái chẵn, vế phải lẻ . Như vậy không thể tìm được hai số nguyên
k và
m
thỏa mãn (4). Trong thang log không có âm
3/2.f0.
Quảng (f; 3/2.f0
) gọi là quảng 5 hoàn toàn( hoăc quảng 5 đúng) .
Nhưng cần phải giữ lại
tính “đều” của thang nhạc để khi chuyến giai điệu không bị méo, còn âm
“hoàn toàn” có tần số đúng 3/2f0
thì được thay nó bằng một âm có tần số giao động
gần nhất chấp nhận được với âm hoàn toàn ( đó chính là ý tưởng “ cải
tiến” của Angdrê. Vecmâyơ) Nghĩa là tìm số hữu tỷ k/m gần đúng với số
vô tỷ log2(3/2)
sao cho sai số tần số tương ứng < 1Hz để tai ta không nhận thấy được.
Để tìm số hữu tỷ gần đúng với số vô
tỷ 21/12
.
Số hữu tỷ
7/12 = 0, 583
gần đúng log2
(3/2)
đạt độ chính xác 0,002
( 1Hz ứng với 0.004
trên thang log2
) với sai số mong muốn không
quá 0,004
. Lấy m = 12,
ta được thang nhạc đều 12 âm, âm thứ 7 rất gần với quảng 5 hoàn toàn (3/2.f0).
Ta có bảng sau :
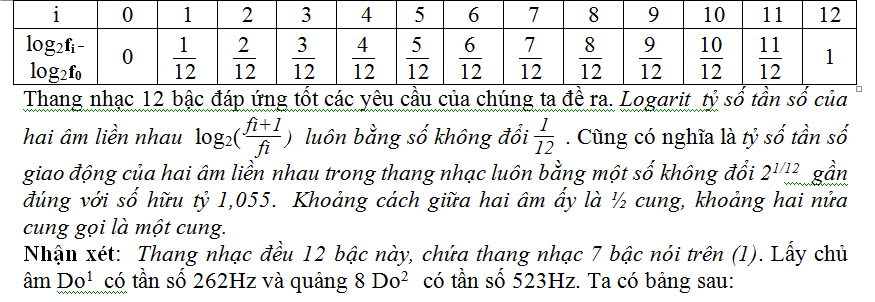
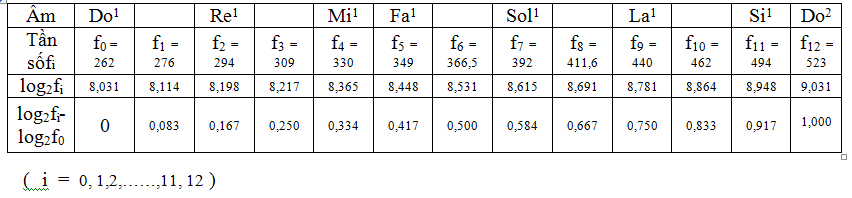
Ngoài 7 âm cơ bản trong quảng 8(Do1 – Do2) , ta còn 5 âm
phụ trong tập hợp vừa đủ 12 bậc của thang. Chúng được ký hiệu bằng cách thêm vào
dấu thăng(#) hoặc dấu giảm( b ) bên cạnh
các âm cơ bản. Ví dụ f1
= Do1# hoặc f3
= Mi1b …
Từ
thang nhạc 7 bậc không đều, sau khi bổ sung thêm 5 âm phụ ta có thang nhạc 12
bậc đều:
( Do , Do#
, Re , Re#, Mi , Fa , Fa# , Son , Son#,
La , La# , Si , Do ) ,
Hoặc ( Do , Reb,
Re , Mib , Mi , Fa ,Sonb, Son , Lab ,
La . Sib . Si , Do )
2. Gam
trưởng, gam thứ trong âm nhạc
1. Định nghĩa , Thang nhạc
7 bậc , trong đó khoảng cách cao độ giữa các âm liên tiếp tính bằng 1 cung hoặc
½ cung thỏa mãn quy luật dưới đây được gọi là một gam trưởng, âm đầu tiên gọi là
chủ âm, ta gọi là gam f0
trưởng:
( f0 , f1,
f2,
f3
f4
f5
f6
f7
= 2f0
)
]
Z]Z]
Z
]Z]
Z
]Z
]Z
1 1 ½ 1 1 1
½ (1)
Nếu thỏa mãn điều kiện sau đây thì gọi là gam thứ ,âm g0
là chủ âm
(g0,
g1,
g2,
g3,
g4,
g5
g6,
g7
= 2g0
)
]
Z
]Z
]Z
]
Z
]
Z
]Z
]Z
1 ½ 1 1 ½ 1
1 (2)
Ví dụ thang nhạc 7 bậc tự nhiên đầu tiên:
(Do1, Re1,
Mi1, Fa1, Sol1, La1, Si1,
Do2 ) là gam Do trưởng ( kí hiệu là C)
]
Z
]Z
]Z
]
Z
]
Z
]Z
]Z
1 1 ½ 1 1 1 ½
Giữ nguyên thứ tự như vậy nhưng cho La1 đứng đầu ta có gam La thứ
( La1,
Si1, Do2, Re2, Mi2, Fa2,
Sol2, La2 )
]
Z
]Z
]Z
]
Z
]
Z
]Z
]Z
1 ½ 1 1 ½ 1
1
2.Dùng dấu thăng(#) đẻ đổi gam
( thay đổi chủ âm). Do sự cần thiết khi phải lên cao hoặc hạ thầp nhưng vẫn giữ
nguyên giai điệu trưởng ( hoặc thứ), ta dùng dấu thăng(#) hoặc giáng(b
)
( f0
. f1
. f2
. f3
. f4 . f5
. f6
. f7(=2f0)).2f1
. 2f2
. 2f3
. 2f4
]
Z]Z]
Z
]
Z
]
Z]
Z
]Z]
Z
]Z]
Z
]Z
1 1 ½ 1
1 1 ½ 1 1 ½ 1
Ví dụ Từ gam Do trưởng: ( Do, Re, Mi, Fa, Son, La, Si , Do ) , Nếu ta
thêm dấu # vào âm Fa (Fa#) thì ta có gam Son trưởng(G):
( Son, La, Si, Do, Re,
Mi, Fa#, Son ) (3)
Hệ quả. Từ nhận xét trên, từ gam
Xon trưởng( G), áp dụng nhận xét trên , nếu ta đặt thêm dấu # vào âm Do ( vẫn
giữ Fa#) ta được gam Re trưởng (D) :
( Re, Mi, Fa#, Son,
La, Si , Do#, Re )
Tương tự , từ gam Re trưởng, nếu
cho Sol# ta có gam La trưởng ( A)…
Dùng dấu giáng (b), ta có nhận xét
sau :Từ gam trưởng f0 nếu ta đặt dấu giáng b vào âm thứ sáu f5b thì
được gam trưởng nhận âm thứ tư làm chủ âm (f3).
Ví dụ, từ gam Do trưởng, nếu cho
Sib ta sẽ được gam Fa trưởng( F) . Tiếp tục, từ gam Fa trưởng (Sib)
nếu cho thêm một dấu giáng vào Mib, ta có gam Sib trưởng
có hai dấu b
là Sib và Mib .
Ta không nói về gam thứ vì đã
có nhận xét trên : một gam trưởng có chủ âm là âm thứ nhất f0
hoặc là gam thứ có chủ âm là âm thứ 6 (f5)
. Từ đó ta có bảng sau đây để xác định gam trưởng, gam thứ theo các dâu thăng
(#) hoặc dấu giáng (b):
Ta có bảng
các gam theo dấu thăng (#) :
Không
có dấu thăng Do trưởng (C ) hoặc
La thứ ( Am)
1 dấu thăng ( Fa#)
Son trưởng(G) hoặc Mi thứ (Em)
2 dấu thăng ( Fa# , Do#)
Re trưởng (D) hoặc Si thứ ( Bm)
3 dấu thăng ( Fa# , Do#,
Son# ) La trưởng (A) hoặc Fa#
thứ (F#m)
4dấu thăng ( Fa#,Do#,Son#,
Re#) Mi trưởng (E) hoặc Do# thứ(C#m)
5
dấu thăng ( Fa#,Do#,Son#,Re#,La#)
Si trưởng(B) hoặc Son# thứ (G#m)
Các gam theo dấu giáng(b)
1 dấu giáng (b) : Sib
Fa trưởng (F) hoặc Re thứ (Dm)
2 dấu giáng (b) : Sib, Mib Sb
trưởn g (Bb) hoặc Son thứ(Gm)
3 dấu giáng(b) : Sib, Mib,
Lab Mib trưởng (Eb)
hoặc Do thứ (Cm)
4 dấu giáng : Sib, Mib,
Lab, Reb Lab
trưởng (Lab) hoặc Fa thứ(Fm)
Áp dụng : Chuyển gam để điều chỉnh
nâng cao hoặc hạ thấp cao độ một bản nhạc thích hợp với giọng hát của mình.
Ví dụ 1, một bản nhạc gam Do trưởng(C) , nếu thấy thầp quá có thể nâng lên một
ton, ta chuyển lên Re trưởng ( D), bản nhạc phải có hai dấu thăng F#
và Do# , mọi âm đều nâng lên một bậc.
Ví dụ 2, một bản nhạc gam Do thứ(Cm) ba dấu giáng Sib, Mib,
Lab, cao quá muốn hạ thấp xuống 2 ton, ta chuyển sang gam La thứ(Am)
bỏ tất cả dấu giáng, cho các nốt nhạc hạ xuống 2 bậc.
3.
Phím đàn
Hai giây
đàn cùng loại có tần số giao động tỷ lệ nghịch với chiều dài của chúng. Nguyên
lý này quyết định việc chế tạo các loại phím trên đàn ghita hoặc mandolin. Thang
nhạcc của chúng ta sử dụng trong một quảng tám có 12 bậc. Khi ta bấm vào phím và
gẫy vào giây sẽ phát ra các âm thanh cao thấp khác nhau bởi vì độ dài của giây
đàn được điều chỉnh khi bấm vào phím đàn. Vấn đề đặt ra là vị trí các phím
trên cần đàn như thế nào? Khoảng cách giữa các phím có đều không? Xét một giây
bất kỳ cua đàn Ghita cũng như Mangdolin , giả sử độ dàì của giây tính từ phím
trên cùng đến con ngựa là 2a, ( khi không dùng tay bấm vào phím nào). Độ dài này
ứng với tàn số âm f0
trong thang nhạc đều 12 bậc Ta kí hiệu di
(
i
=
0,1,….)
là độ dài của giây ứng với fi
trong thang nhạc.Ta biết rằng dãy { f0,
f1,
……., fm,
} là một cấp số nhân công bội q = 21/12 gần bằng 1,056. Theo định
luật âm học, tần số giao động của âm thanh tỷ lệ nghịch với độ dài của giây. Vì
vậy dãy tương ứng { a0,
a1,
……., am
}
là một cấp số nhan có công bội q’ = 1/q
= 2-1/12 ; a0 = 2a
.
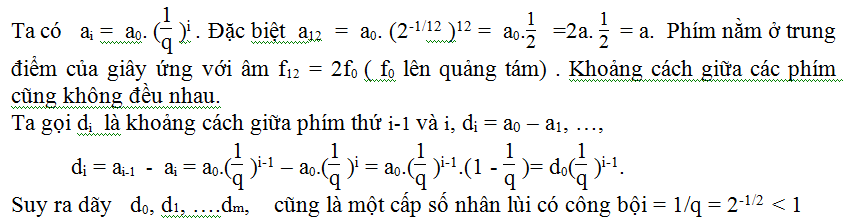
Tài
liệu tham khảo
1. Gam đơn giản GE Shilov (bản dịch viết tay của Hoàng Trọng Thái)
2. Vật lý & âm nhạc - Glep Anfilov (NXB KH & Kỷ thuật/HN 1978)
3. Nhạc lý nâng cao - Ngô Ngọc Thắng (NXB Âm nhạc HN 1997
Trần
Đình Viện,
Hà
Nội, ngày 27/4/2011
|
